Levy曲线是将一条线段不停地分形成两条长度相等且相互垂直的线段而生成的。Levy分形的最后很像一个英文字母C,所以也称它为C曲线。 Levy曲线的生成示意如图1所示。
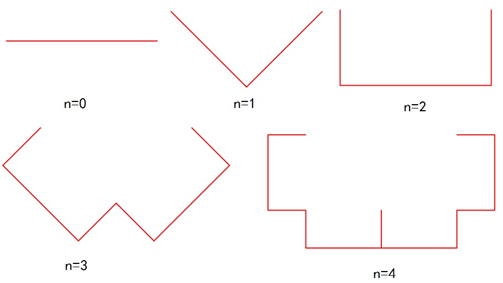
图1 Levy曲线的生成
1.Levy曲线
Levy曲线采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>Levy曲线</title>
</head>
<body>
<canvas id=”myCanvas” width=”600″ height=”400″>
</canvas>
<script type=”text/javascript”>
var canvas = document.getElementById(‘myCanvas’);
var ctx = canvas.getContext(‘2d’);
var depth=12;
ctx.lineWidth = 2;
fractal_c(depth,{x:150,y:100},{x:450,y:100});
function fractal_c(n,p1,p2)
{
if (n>0)
{
var x3=(p1.x+p1.y+p2.x-p2.y)/2;
var y3=(p2.x+p2.y+p1.y-p1.x)/2;
fractal_c(n-1,p1,{x:x3,y:y3});
fractal_c(n-1,{x:x3,y:y3},p2);
}
if (n==0)
{
ctx.strokeStyle = “red”;
ctx.beginPath();
ctx.moveTo(p1.x,p1.y);
ctx.lineTo(p2.x,p2.y);
ctx.closePath();
ctx.stroke();
}
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的Levy曲线,如图2所示。

图2 递归深度depth =12的Levy曲线
将上面HTML文件中的调用语句“fractal_c(depth,{x:150,y:100},{x:450,y:100}); ”修改为“fractal_c(depth,{x:350,y:100},{x:350,y:300});”,则可在浏览器窗口中绘制出如图3所示的Levy曲线,它很像字母C。

图3 C曲线
2.龙形曲线
Levy曲线是将一条线段不停地分形成两条长度相等且相互垂直的线段而生成的,分形是对折方向都是沿着同一个方向。如果将分形对折方向进行交替切换会如何呢?绘制出的曲线像龙形,称为龙形曲线。
龙形曲线的生成方式与Levy曲线相似,也是将线段不停地分形成两条长度相等且相互垂直的线段,不同之处是其对折的方向是一个左一个右,而levy曲线则是始终朝着一边对折。龙形曲线的生成示意如图4所示。
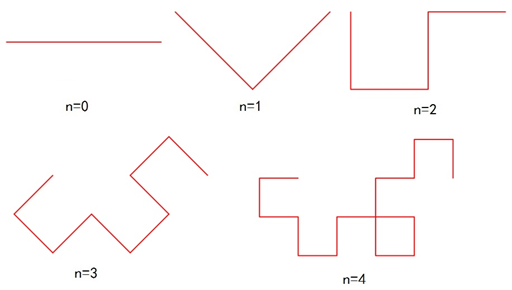
图4 龙形曲线的生成
龙形曲线采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>龙形曲线</title>
</head>
<body>
<canvas id=”myCanvas” width=”600″ height=”400″>
</canvas>
<script type=”text/javascript”>
var canvas = document.getElementById(‘myCanvas’);
var ctx = canvas.getContext(‘2d’);
var depth=10;
ctx.lineWidth = 2;
fractal_c(depth,{x:150,y:150},{x:450,y:150},true);
function fractal_c(n,p1,p2,left)
{
if (n>0)
{
if (left)
{
var x3=(p1.x+p1.y+p2.x-p2.y)/2;
var y3=(p2.x+p2.y+p1.y-p1.x)/2;
}
else
{
var x3=(p1.x+p2.y+p2.x-p1.y)/2;
var y3=(p1.x+p2.y+p1.y-p2.x)/2;
}
fractal_c(n-1,p1,{x:x3,y:y3},true);
fractal_c(n-1,{x:x3,y:y3},p2,false);
}
if (n==0)
{
ctx.strokeStyle = “red”;
ctx.beginPath();
ctx.moveTo(p1.x,p1.y);
ctx.lineTo(p2.x,p2.y);
ctx.closePath();
ctx.stroke();
}
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的龙形曲线,如图5所示。

图5 递归深度depth =10的龙形曲线
3.变形的Levy曲线
为了绘制Levy曲线,还可以编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>变形的Levy曲线</title>
</head>
<body>
<canvas id=”myCanvas” width=”600″ height=”400″>
</canvas>
<script type=”text/javascript”>
var canvas = document.getElementById(‘myCanvas’);
var ctx = canvas.getContext(‘2d’);
var d=45;
ctx.lineWidth = 2;
ctx.strokeStyle = “red”;
ctx.beginPath();
ctx.moveTo(400,100);
drawC(400,100,150,90+45);
ctx.stroke();
function drawC(x,y,L,angle)
{
if (L>=5)
{
var x1=x+L*Math.cos(angle*Math.PI/180);
var y1=y+L*Math.sin(angle*Math.PI/180);
drawC(x,y,L*0.707,angle-d);
drawC(x1,y1,L*0.707,angle+d);
}
else
{
ctx.lineTo(x,y);
}
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的Levy曲线,如图6所示。
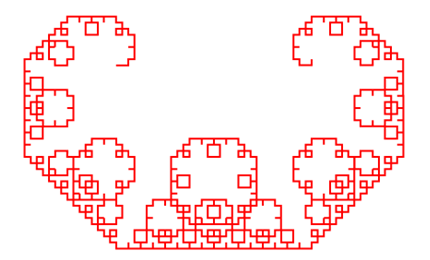
图6 d=45时的Levy曲线
上面程序中的d取不同值时,所绘制的曲线会变化。下图7~9分别是d值取75、90和150时绘制的曲线。
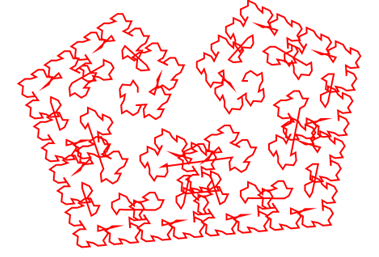
图7 d=75时的Levy曲线

图8 d=90时的Levy曲线

图9 d=150时的Levy曲线
1.《JavaScript图形实例:Levy曲线及其变形》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《JavaScript图形实例:Levy曲线及其变形》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.cxvn.com/study/26956.html